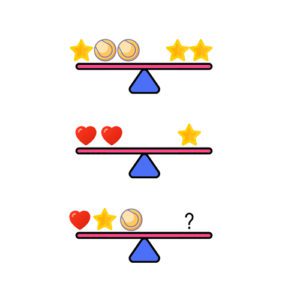
Начнём с простого: сколько мячей нужно положить на правую сторону, чтобы сохранить баланс?

Дана арифметическая прогрессия: 9, b, с, 18. Чему равно c?
В семье старший ребёнок — мальчик. Какова вероятность того, что младший тоже мальчик?
Из бочки вина перелили ложку вина в (неполный) стакан с чаем. А потом такую же ложку смеси из стакана — обратно в бочку. Теперь и в бочке, и в стакане имеется некоторый объём посторонней жидкости (вина в стакане, чая в бочке). Где объём посторонней жидкости больше: в стакане или в бочке?
На склад приехало 800 тонн угля в 28 вагонах трёх ёмкостей: по 15 т, 20 т и 30 т. Вагонов каждой ёмкости приехало как минимум по одному. Сколько приехало вагонов ёмкостью 30 тонн?
В шкафу лежат вперемешку 5 пар светлых ботинок и 5 пар тёмных ботинок одинаковых размера и фасона. Какое наименьшее количество ботинок надо взять наугад из шкафа, чтобы среди них была хоть одна пара (на правую и левую ноги) одинакового цвета?
Удав, которому 110 лет, беседует с черепахой, чей возраст нам неизвестен.
— Сколько тебе лет? — спрашивает удав.
— Мне в 10 раз больше, чем было тебе, когда мне было, как тебе сейчас. — отвечает черепаха.
Сколько лет черепахе?
Посчитайте результат:
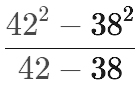
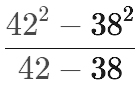
Используйте для этого уравнение:
![]()
![]()
Есть колония Бактерий. Очень большая – N штук… Или нет, целых M штук! В ней поселяется Вирус. Каждую секунду Вирус жрет одну бактерию, и, наевшись, тут же делится на два себе подобных. Бактерии питаются всем подряд (не бактериями и не вирусами, конечно) и тоже каждую секунду делятся пополам. Сожрёт ли когда-нибудь Вирус все Бактерии?
Поздравляем с прохождением теста! А теперь предлагаем почитать статьи по программированию на Python на нашем сайте PythonTurbo!
